From quantum geometry to non-linear optics: recent advances in topological band theory

By Tomáš Bzdušek, University of Zurich

Topological principles constitute at present an integral component of condensed matter physics, deeply influencing the modern characterization of electronic states while also guiding materials design. In this Perspective, I highlight three research threads in single-particle topological band theory that have recently gained momentum while fruitfully nurturing each other: (i) the rise of the quantum geometric tensor, whose symmetric (quantum metric) and antisymmetric (Berry curvature) parts can at present be directly accessed with optical probes; (ii) the notions of delicate and multigap topology that fall outside the established paradigms of tenfold way and symmetry-based indicators yet leave robust physical fingerprints; and (iii) the introduction of higher-form topological structures, borrowed from string theory, that generate a quantized contribution to non-linear optical responses.

Quantum geometric tensor

While Berry curvature of Bloch states has become an established concept in condensed matter physics, entering the description of band topology as well as semiclassical transport [1], recent years have witnessed a revival of interest in a further geometric aspect of energy bands: their quantum (or Fubini-Study) metric. Both quantities measure aspects of how the wave function changes when varying momentum. Specifically, Berry curvature quantifies the complex phase acquired by the state when it is evolved on a small closed loop in momentum space; in contrast, quantum metric measures how quickly the state grows in orthogonal directions when departing away from an initial momentum.

Both Berry curvature [2] and quantum metric [3] can be extracted as components of a single mathematical object: the quantum geometric tensor (QGT). Assuming a single non-degenerate band $|u_n>$ that depends on momentum $k$, QGT is defined as the gauge-invariant Hermitian matrix [4]

$$Q_{\mathit{𝑎𝑏}}^n=<{\partial }_a{u}_n|\left(1-|u_n><u_n|\right)|{\partial }_b{u}_n>,$$

where ${\partial }_a$ indicates the derivative of the state with respect to the momentum component $k_a$. In two dimensions, this amounts to a $2\times 2$ matrix with complex entries. The QGT naturally decomposes in the following way [5]: its symmetric real part is the quantum metric ($g_{\mathit{𝑎𝑏}}^n$) and its antisymmetric imaginary part is proportional to the Berry curvature ($F_{\mathit{𝑎𝑏}}^n$) of the band $|u_n>$. Although QGT has been recognized as a property of Bloch energy bands for decades, it has recently moved into the spotlight due to relations of its components to optical responses, to electron-phonon coupling [6], and to superfluid weight in flat-band superconductors [7, 8].

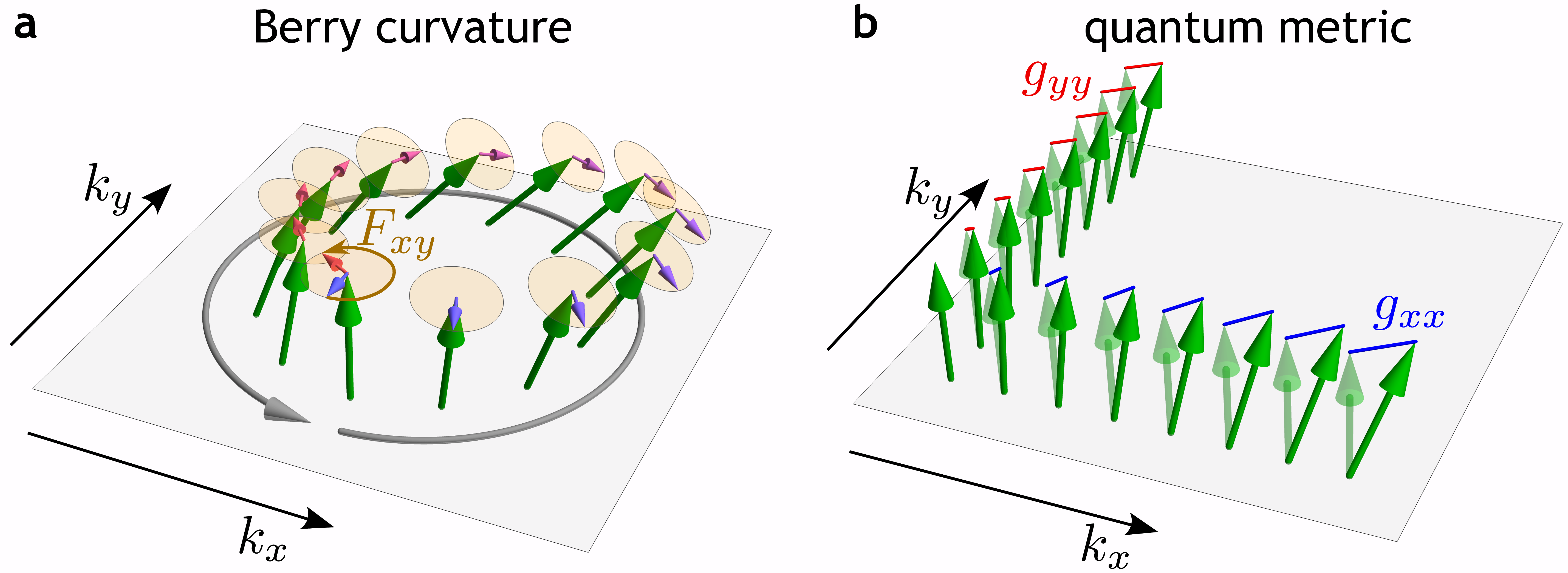
Berry curvature and quantum metric are not entirely independent. Notably in two dimensions, where Berry curvature has only a single component, this component is bounded in absolute value by the determinant of the quantum metric ($\left|F\right|\le 2\sqrt{\det <!--\; FUNCTION\; APPLICATION\; -->g}$) at every momentum $k$ [9]. Correspondingly, a suitably defined (and non-quantized) integral of the quantum metric, called the quantum weight ($K$) [10], is bounded to be larger than the quantized integral of the Berry curvature (the Chern number, $C$).

Further and less obvious constraints follow from considering optical responses, suggesting a deeper link between topology, quantum metric, and response theory. In particular, the linear optical conductivity can be related using the Kubo-Greenwood formula to an integral involving inter-band Berry connection (also called optical dipole) $A_a^{\mathit{𝑛𝑚}}=<u_n|{\partial }_a{u}_m>$ that combines information about the geometry of occupied and unoccupied energy bands [11]. Careful analysis along the outlined logic results in a non-trivial bound on the possible size of a topological energy gap: defining an optical weight $W^0$ as the integral over all frequencies of the real part of the optical conductivity $\mathit{𝑅𝑒}[{\sigma }_{\mathit{𝑥𝑥}}(\omega )]$ of a two-dimensional insulating system and taking $C$ to be its Chern number, the energy gap was shown to obey the strict bound [10]

$$\mathrm{\Delta }\le \frac{4{\hslash }^2{W}^0}{e^2\left|C\right|}.$$

Following this line of reasoning [10, 12], it is further shown that integrals of quantum metric and of Berry curvature specify negative moments of the optical conductivity: the integral of $\mathit{𝑅𝑒}[{\sigma }_{\mathit{𝑎𝑎}}(\omega )]∕\omega$ amounts to the quantum weight $K$, while the integral of $\mathit{𝐼𝑚}[{\sigma }_{\mathit{𝑎𝑏}}(\omega )]∕\omega$ amounts to the Chern number $C$.

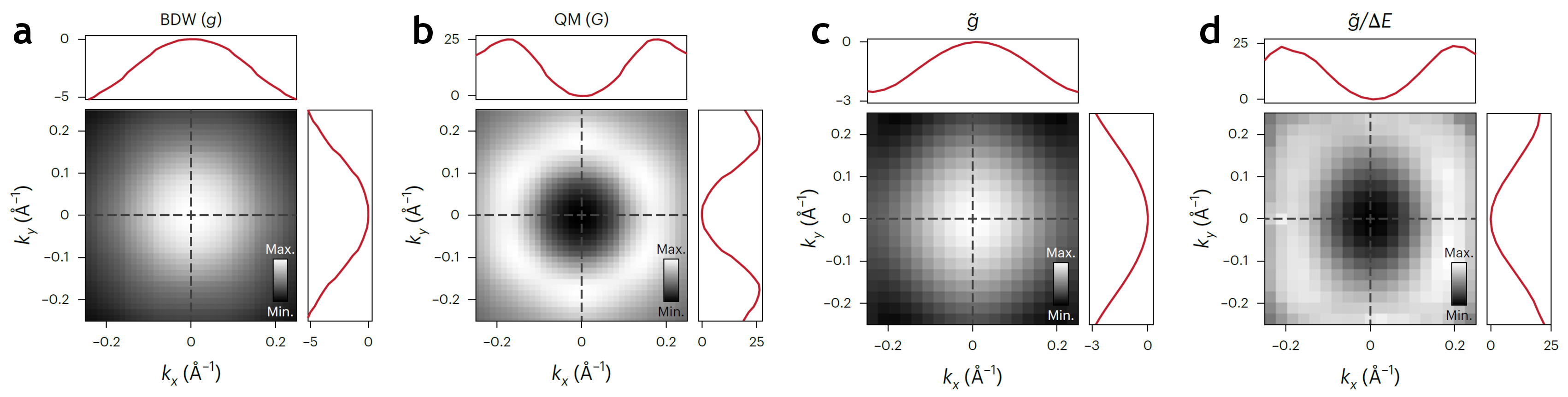
Very recently, the relations between the components of QGT and optical responses have been turned around: the work of Ref. 13 proposed a protocol for momentum-resolved spectroscopic probing of QGT in 2D materials. Their starting point is that QGT of band $|u_n>$ with energy $E_n$ can be expanded using all eigenstates and eigenenergies of the Bloch Hamiltonian $H$ as

$$Q_{\mathit{𝑎𝑏}}^n=\sum _{m\ne n}\frac{<u_n|{\partial }_{a}H|u_m><u_m|{\partial }_{b}H|u_n>}{{(E_m-E_n)}^{\alpha }}$$

with exponent $\alpha =2$. The key insight here is that the same expression with the exponent set to $\alpha =1$, dubbed quasi-QGT (labeled $q_{\mathit{𝑎𝑏}}^n$), is conveniently accessible in experiments: its real part (the band Drude weight) can be estimated from band dispersion, accessible in conventional angle-resolved photoemission spectroscopy (ARPES), while its imaginary part (the orbital angular momentum) is accessed by circular dichroism (CD)-ARPES, in which one measures the difference in photoemitted electron intensity under using right-handed and left-handed circularly polarized light. Assuming an effective two-band approximation for the bands nearest to the Fermi level, the two tensors are related by simple rescaling $Q_{\mathit{𝑎𝑏}}^n=q_{\mathit{𝑎𝑏}}^n∕\mathrm{\Delta }E$, with the $k$-dependent energy gap $\mathrm{\Delta }E$ readable from ARPES. The authors successfully illustrated their protocol with an application to the quasi-two-dimensional kagome material CoSn. The outlined experimental protocol was further advanced with the subsequent work of Ref. 14, which extracted the quantum metric tensor of the valence band of black phosphorus without resorting to the auxiliary quasi-QGT. Such a simplification was achieved by reconstructing the pseudospin texture by means of polarization-resolved ARPES measurements.

Curiously, the relevance of QGT to optics does not terminate with linear (first-order) responses, but it extends to non-linear (second-order) responses as well. In fact, the recent formulation of these higher-order phenomena revealed previously unrecognized topological aspects of band theory in three dimensions. To illuminate these aspects, it turned out to be valuable to study few-band toy models with so-called unstable topological invariants.

Delicate and multigap topology

The ‘stability’ of a topological invariant means that (i) the invariant can be defined in models with an arbitrarily large number of energy bands and that (ii) it cannot be trivialized through the addition of a trivial band (specifically: of an atomic limit) to either the occupied or the unoccupied sector. Stable topological invariants have been extensively classified across a broad range of symmetry settings (including Altland-Zirnbauer symmetry classes, various spatial dimensions, and space groups) with the language of symmetry-based indicators [15, 16] and elementary band representations [17] providing particularly valuable insights for first-principles calculations and materials design. (So-called fragile topology [18] corresponds to an intermediate scenario where the topological obstruction can be removed by including a trivial band to the occupied—but not by adding it to the unoccupied—part of the spectrum.)

Nevertheless, there are instances of refined topological invariants that only apply to models with a small total number of energy bands (delicate topology) or to models where the bands are partitioned by more than one energy gap (multigap topology). A long-standing example of delicate topology is the Hopf insulator [19]: a two-band model of a three-dimensional magnetic topological insulator which for over a decade resisted integration into a broader classification principle. Its topological invariant (the Hopf invariant) $h\in \mathbb{Z}$ is expressed elegantly as the integral of $𝐀\cdot 𝐅$, i.e., of the dot product of the Berry connection and Berry curvature of the occupied band. This integral is quantized only in two-band models.

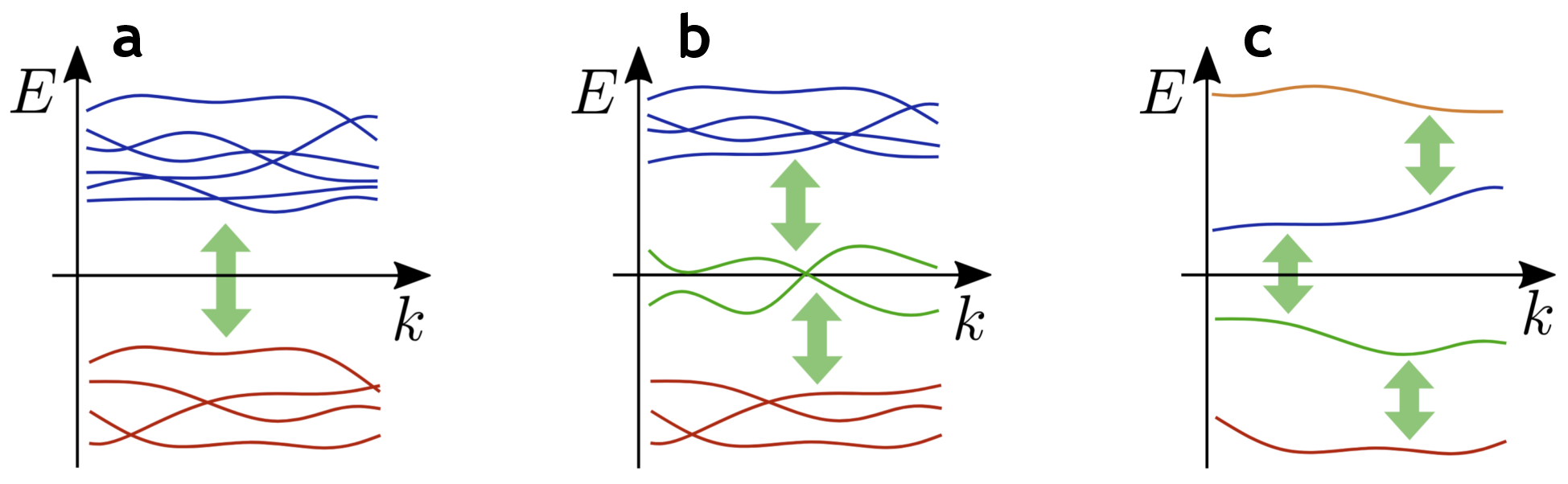
Multigap topology got onto the scene with the discovery of non-Abelian braiding of band degeneracies in the momentum space of spinless $\mathit{𝑃𝑇}$-symmetric materials [20], i.e., those that have combined space-time-inversion symmetry and negligible spin-orbit coupling. Specifically, while Dirac points in 2D band structures (such as that of graphene) carry a non-trivial value of a ${\mathbb{Z}}_2$ invariant (namely, a quantized Berry phase), whether a pair of Dirac points actually annihilate upon collision or not is dictated by their braiding around Dirac points in adjacent energy gaps. This reciprocal braiding of Dirac points in momentum space [21], experimentally demonstrated with acoustic meta-materials [22], is captured by assigning each Dirac point a non-Abelian invariant with values in the algebra of Pauli operators $\{\pm 1,\pm i{\sigma }_x,\pm i{\sigma }_y,\pm i{\sigma }_y\}$: Dirac points in one energy gap carry ‘charge’ $\pm i{\sigma }_x$ while those in an adjacent energy gap carry ‘charge’ $\pm i{\sigma }_y$. The non-trivial braiding follows from the non-commutativity ${\sigma }_x{\sigma }_y=-{\sigma }_y{\sigma }_x$.

Abundant examples of unstable invariants have been characterized over the past five years. In few-band systems with mirror symmetry, given certain condition on mirror eigenvalues of the energy bands, returning Thouless pump $\mathit{𝑅𝑇𝑃}\in \mathbb{Z}$ invariant can be defined [23], which corresponds to a quantized Chern number on half of the Brillouin zone (which is reverted on the complementary half). Furthermore, spinless $\mathit{𝑃𝑇}$-symmetric systems turned out to be a particularly fertile ground for delicate and multigap topology. Beyond the already introduced non-Abelian invariant, any pair of bands in 2D can carry an Euler class $𝜀\in \mathbb{Z}$ [21]. Non-zero value of $𝜀$ leads to fingerprints in QGT [24] and implies that the bands must be tied together with a minimum of $2\left|𝜀\right|$ Dirac points. Further invariants (Hopf invariants, Pontryagin invariants, and isoclinic winding numbers) were introduced for collections of bands in three dimensions [25–27].

While such unstable topological models appear to be rather remote from applications to realistic materials, valuable insights were gained by considering their non-linear optical properties. Specifically, the shift current constitutes a dc-response of non-centrosymmetric crystals to an ac-field of the form

$$j_a(0)={\sigma }_{\mathit{𝑎𝑏𝑐}}^{\mathit{𝑠h𝑖𝑓𝑡}}(\omega )E_b(-\omega )E_c(\omega ).$$

It was reported [28] that models with RTP invariant allow for a quantized contribution to the integral $\int \mathit{𝑑𝜔}{\sigma }_{\mathit{𝑎𝑏𝑏}}^{\mathit{𝑠h𝑖𝑓𝑡}}(\omega )$ for suitable orientation of the axes $a$ and $b$. Furthermore, the integrated circular shift photoconductivity in three-dimensional models is quantized if any of the broad range of unstable invariants in three-dimensional $\mathit{𝑃𝑇}$-symmetric setups acquires a non-trivial value [29]. Remarkably, the mathematical descriptions developed in this context, phrased in terms of higher-form topological structures, provide hints for transferring these quantization results towards realistic materials, as described further below.

However, two points merit clarification before proceeding. First, the shift current in real materials includes multiple contributions [31]; namely, those induced by interband electron-hole excitations via absorption of photons (${\mathit{𝑠h𝑖𝑓𝑡}}_{\mathit{𝑒𝑥𝑐}.}$), those induced by intraband relaxation via scattering with phonons and impurities (${\mathit{𝑠h𝑖𝑓𝑡}}_{\mathit{𝑖𝑛𝑡𝑟𝑎}.}$), and those induced by recombination of electron-hole pairs (${\mathit{𝑠h𝑖𝑓𝑡}}_{\mathit{𝑟𝑒𝑐}.}$). The reported quantized contributions [28, 29] relate solely to the ‘excitation’ part of the shift current. Whether this contribution dominates the non-linear response depends on the specific material. Second, non-centrosymmetric crystals admit asymmetric excitation and scattering rates, enabling a further contribution to the dc-response called the ballistic current [32]. In the subsequent text, we simplify the discussion by focusing solely on the excitation part of the shift current, which is found to be of topological nature.

Higher-form topological structures

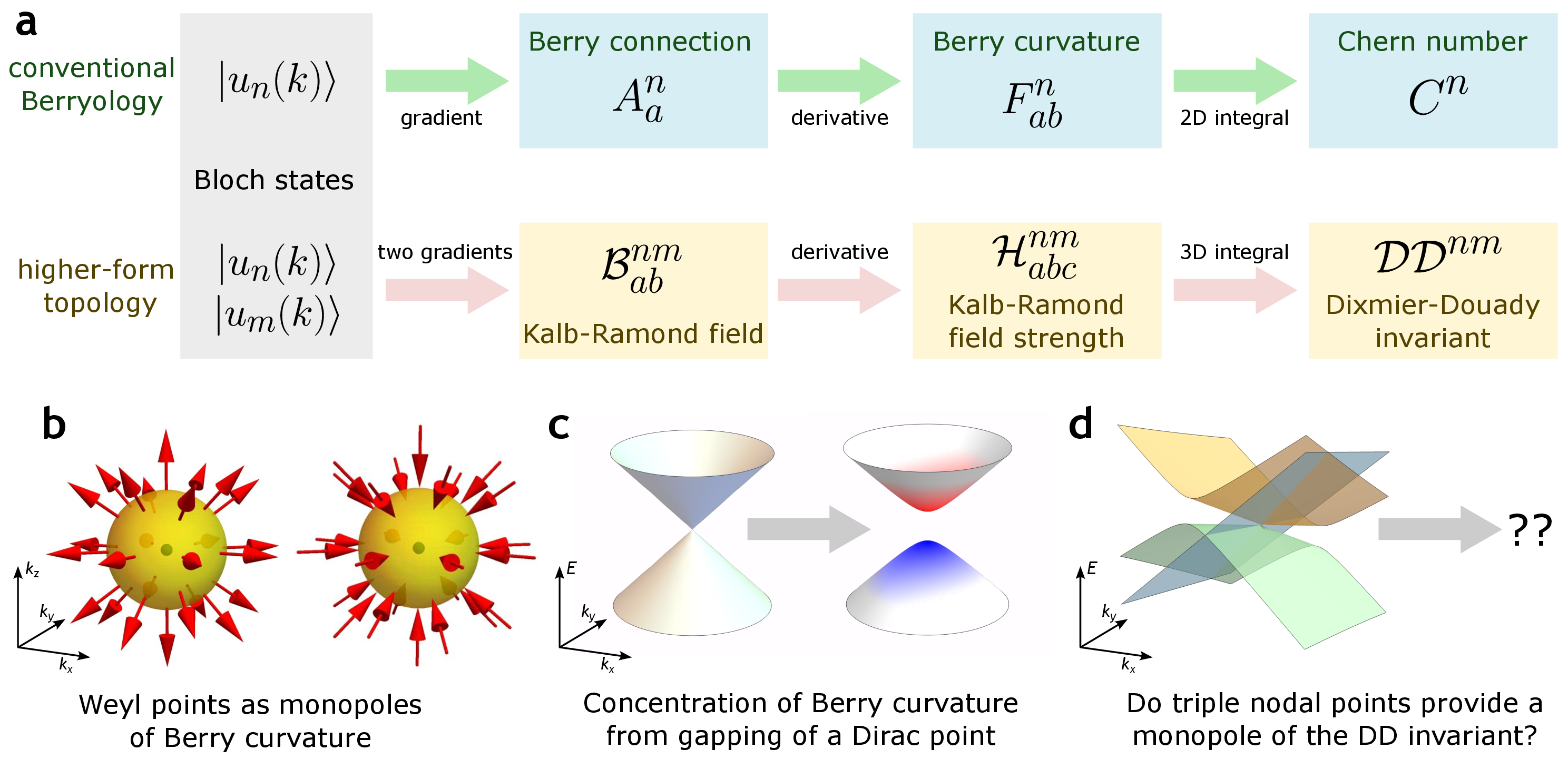
To introduce the higher-form topology lurking behind the quantized contributions to non-linear optical responses, it is insightful to review the key mathematical objects in the context of ‘Berryology’. The determination of Berry curvature can be understood as a three-step process: first, find Bloch states $|u_n>$ in a smooth gauge in some region of the momentum space; second, compute the Berry connection $A_a^n=i<u_n|{\partial }_a{u}_n>$ using the derivatives of the state; and third, compute the Berry curvature $F_{\mathit{𝑎𝑏}}^n={\partial }_a{A}_b^n-{\partial }_b{A}_a^n$ as an antisymmetrized derivative of the connection. If a gauge transformation is applied to the Bloch states, the Berry connection is altered, yet the Berry curvature remains unchanged. This is mathematically analogous to the way the scalar and the vector potential in electromagnetism are changed by gauge transformations while the electric and magnetic fields remain invariant.

Here is how the same steps are presented in mathematical literature: The (continuous) association of momenta $k$ to Bloch states $|u_n(k)>$ is called a vector bundle, since a vector (in the Hilbert space) is assigned to each momentum $k$. The notions of connection and curvature can be defined generally for any vector bundle; for example, considering vectors tangent to a two-dimensional surface results in the usual geometric (i.e., Gaussian) curvature of the surface. The (anti-)symmetrization of the derivatives is important as it ensures that the studied objects are differential forms, whose integrals obey variants of Stokes’ theorem. Specifically, the Berry connection is described as a $1$-form because it involves one derivative, while the Berry curvature is a $2$-form due to the involvement of two derivatives.

The key idea behind higher-form topology is to find analogous mathematical objects where all the indices are increased by one. Namely; is it possible to construct a ‘higher-form connection’ (which involves two derivatives and that changes under gauge transformations) whose derivative gives a ‘higher-form curvature’ (which involves three derivatives and that is gauge-invariant)? The answer is affirmative, with the sought objects appearing in the integrated circular shift photoconductivity [27] (specifically, as alluded earlier, in the ‘excitation’ contribution to the shift current). The final expression (modulo unspecified coefficients and minus symmetrization over indices) takes the form

$$\int \; <!--\; nolimits\; -->\mathit{𝑑𝜔}{\sigma }_{\mathit{𝑎𝑏𝑐}}^{\mathit{𝑠h𝑖𝑓𝑡},C}(\omega )\propto {\int \; <!--\; nolimits\; -->}_{\mathit{𝐵𝑍}}{d}^{3}k\sum _{n\in \mathit{𝑜𝑐𝑐}.}\sum _{m\in \mathit{𝑢𝑛𝑜𝑐𝑐}.}{H}_{\mathit{𝑎𝑏𝑐}}^{\mathit{𝑛𝑚}}$$

with the summations taken over all occupied and unoccupied bands. While the object $H_{\mathit{𝑎𝑏𝑐}}^{\mathit{𝑛𝑚}}$ on the right-hand side was originally formulated in terms of derivatives of the interband Berry connection [11], here I follow the more recent and mathematically cleaner description in terms of gerbe bundles and tensor connections [33] borrowed from string theory literature [34]. For simplicity, I will focus on spinless $\mathit{𝑃𝑇}$-symmetric models. Because a bulk shift current generally requires broken inversion, the condition “$\mathit{𝑃𝑇}$ present with $P$ broken” implies $T$ is broken (for example by antiferromagnetic order) while the combined $\mathit{𝑃𝑇}$ symmetry remains intact.

To begin, one needs to introduce triplets of scalar fields $({\varphi }_1^{\chi },{\varphi }_2^{\chi },{\varphi }_3^{\chi })$—which define a gerbe—in momentum space [35], with $\chi$ the ‘flavor’ of the fields. Fixing an occupied band $|u_n>$ and an unoccupied band $|u_m>$, and letting the flavor $\chi$ correspond to orbitals within a unit cell, two of the fields are chosen as ${\varphi }_1^{\chi }(k)=<\chi |u_n(k)>$ (i.e., the orbital-$\chi$ component of $|u_n>$) and as ${\varphi }_2^{\chi }(k)=<u_m(k)|\chi >$. The remaining field ${\varphi }_3^{\chi }(k)$ is defined as a line integral of the inter-band connection (optical dipole) $A_{\mathit{𝑛𝑚}}$ on a suitably defined path that terminates at $k$. These three fields are real due to the assumed spinless $\mathit{𝑃𝑇}$ symmetry. One then combines the fields into a tensor connection (also called the Kalb-Ramond field)

$$B_{\mathit{𝑎𝑏}}^{\mathit{𝑛𝑚}}\propto {𝜖}_{\mathit{𝑖𝑗𝑘}}\sum _{\chi }{\varphi }_i^{\chi }{\partial }_a{\varphi }_j^{\chi }{\partial }_b{\varphi }_k^{\chi }$$

where ${𝜖}_{\mathit{𝑖𝑗𝑘}}$ is the fully antisymmetric symbol. The connection $B$ combines geometric information about the occupied and unoccupied Bloch states in a non-trivial way.

The three fields ${\varphi }_i^{\chi }$ as well as the tensor connection $B$ all change under gauge transformation of the Bloch states; however, the symmetrized derivative

$$H_{\mathit{𝑥𝑦𝑧}}^{\mathit{𝑛𝑚}}={\partial }_x{B}_{\mathit{𝑦𝑧}}^{\mathit{𝑛𝑚}}+{\partial }_y{B}_{\mathit{𝑧𝑥}}^{\mathit{𝑛𝑚}}+{\partial }_z{B}_{\mathit{𝑥𝑦}}^{\mathit{𝑛𝑚}}$$

called the Kalb-Ramond field strength (or curvature $3$-form) is invariant under gauge transformations. In the presence of $\mathit{𝑃𝑇}$, the Kalb-Ramond field can be non-zero only in models with three or more energy bands. Importantly, the integral

$${\mathrm{𝒟𝒟}}^{\mathit{𝑛𝑚}}=-\frac{1}{4{\pi }^2}{\int \; <!--\; nolimits\; -->}_{\mathit{𝐵𝑍}}{d}^{3}k{H}_{\mathit{𝑥𝑦𝑧}}^{\mathit{𝑛𝑚}},$$

(1)

which enters the integrated circular shift photoconductivity, is an integer called the Dixmier-Douady invariant of the bands $|u_n>$ and $|u_m>$. From the experimental vantage point, if the $\mathrm{𝒟𝒟}$ invariant is nonzero, the integrated circular shift photoconductivity changes sign under swapping the pump helicity and is stable to gentle band-structure perturbations that keep the gap. In spinless $\mathit{𝑃𝑇}$-symmetric systems with non-degenerate bands, every pair of bands $n,m$ is characterized by a $\mathrm{𝒟𝒟}$ invariant (although they are not all independent of each other). In the presence of band degeneracies, quantization is only ensured if one sums contributions over all degenerate bands.

Outlooks

The introduction of higher-form topological structures in the description of optical responses invites a lot of questions which at present remain to be investigated. For example, recall that Weyl points in 3D act as monopoles of Berry curvature and that opening a gap in Dirac points in 2D through symmetry-breaking generates a half-quantum concentration of Berry curvature near the avoided crossing. What are the analogous minimal models for solid-state realizations of ‘Kalb-Ramond monopoles’? Since a minimum of three bands are necessary to generate the $\mathrm{𝒟𝒟}$ invariant in $\mathit{𝑃𝑇}$-symmetric models, it seems natural to start searching for strong concentrations of higher-form curvature (and of unusually strong circular shift currents) in antiferromagnetic crystals hosting three-fold band degeneracies [36]. Delicate and multigap topological models could provide valuable insights towards design principles for realistic materials with strong non-linear optical responses: while their unstable topology is typically lost upon the inclusion of additional bands, the $\mathrm{𝒟𝒟}$ invariant can remain unaffected by such changes. Furthermore, while the phenomenology as described above applies directly to spinless $\mathit{𝑃𝑇}$-symmetric systems, analogous phenomena can also be studied in spinful and time-reversal-symmetric models. More broadly, it should be interesting to attempt a systematic tabulation of delicate and multi-gap invariants in the presence of crystalline symmetries, and to investigate whether the remaining contributions (‘intraband’ and ‘recombination’) to this shift current or the ballistic current similarly support a deeper topological formulation.

The early stage of this line of research suggests that impactful contributions can be achieved across all segments of the discovery process, ranging from mathematical characterization and space-group symmetry analysis, through toy models and materials design, to experimental measurements. The Swiss research community, including the MaNEP network, is ideally positioned to contribute to this emerging research avenue, as it includes all the necessary elements for effective investigation of quantum geometry and topology in general and of non-linear optical properties of solids specifically. In particular, University of Zurich and ETH Zurich provide an expert basis for untangling the mathematical aspects of higher-form topology, which can be ideally combined with the strong first-principles modeling capability based at EPFL. This theoretical component can be supplemented with materials synthesis and conductivity probes across multiple labs and facilities in Switzerland as well as with ARPES studies of candidate materials at PSI. In concert, these capabilities can deliver definitive tests of QGT-based bounds and $\mathrm{𝒟𝒟}$-quantized shift currents, providing a route toward practical materials with large bulk photovoltaic responses.

Acknowledgments

The author would like to express gratitude to Aris Alexandradinata, Wojciech Jankowski, Titus Neupert, Robert-Jan Slager, and Bohm-Jung Yang for valuable discussions on the presented topics and for their feedback on a draft of this Scientific Perspective.

References