Spin Resonance in an Unconventional Superconductor

By Daniel Mazzone, Paul Scherrer Institut
Based on article published in Physical Review Letters
Most superconducting condensates are accurately described within the scope of the BCS-theory (Bardeen-Cooper-Schrieffer), where electrons are bound together via virtual phonons. They are in strong contrast to so-called unconventional superconductors, in which the pairing mechanism is still unclear but thought to arise from magnetic fluctuations. Unconventional superconductors feature electronic gap functions with nodal lines or points in reciprocal space, where lowenergy quasiparticles exist and probably play an important role in the formation of Cooper pairs. Many of these condensates possess a prominent magnetic excitation – often called spin resonance – that emerges below the superconducting transition temperature and whose energy scales with the superconducting gap size [1]. This provides evidence that this resonance is deeply connected to the fluctuations triggering superconductivity in these materials.
In our study we answer the fundamental question how the spin resonance is affected when magnetic order is developed inside the superconducting phase. Nd0.05Ce0.95CoIn5 features a superconducting phase with a well-established d-wave symmetry and Tc = 1.8 K that is coexisting with magnetic order below TN = 0.8 K. Using inelastic neutron scattering, we observe a superconducting spin resonance that appears along the nodal direction of the superconducting gap and that is not altered by static magnetic order (see Fig.) [2]. This is unexpected as long-range magnetic order usually breaks the rotational symmetry that, in turn, modifies the excitation spectrum. Our results show that the spin resonance in Nd0.05Ce0.95CoIn5 is a longitudinal mode with fluctuations oriented along the ordered magnetic moments arising below TN.
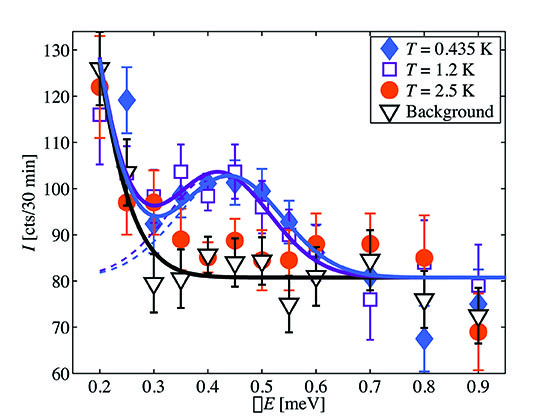
Figure: Neutron excitation spectrum measured along the superconducting d-wave gap at T = 0.44, 1.2 and 2.5 K. Taken from [2].© PSI
Reference:
[1] G. Yu et. al Nat. Phys. 5, 873 (2009).
[2] D. G. Mazzone et. al Phys. Rev. Lett. 119, 187002 (2017).