Metal with chains
The microscopic distinction between ordinary insulators and metals is understood since the early years of quantum mechanics by the so-called band theory. Semimetals form a natural boundary between the two, and they attracted much attention in recent years due to their unusual electronic structure. Now, a team of physicists from ETH Zürich has proposed a new class of semimetals which should exhibit unusual magnetoeletric properties and anomalous Hall effect on the surface.

By Tomáš Bzdušek, Department of Physics, ETH Zürich
Based on article published in Nature
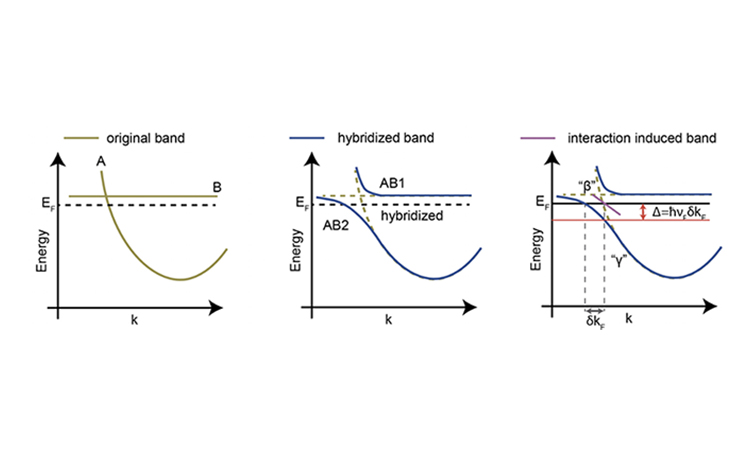
Band structures can be classified as metallic or insulating. In metals, an infinitesimally small amount of energy can excite the electrons and trigger electric current, while in insulators there is a finite energy gap preventing such dynamics.
From the mathematical perspective, an insulator is not very different from vacuum. The energy barrier of an insulator corresponds to the mass of an electron, Egap ~ 2mc2, and both can be described by the massive Dirac equation. However, while a high-energy physicist cannot adjust the fundamental constants of nature, a condensed-matter physicist can change the “electron mass” simply by straining the crystal or by modifying the chemical composition. Notably, the electron mass can be made negative, which corresponds to topological insulators.
Certain crystalline symmetries can fix the effective electron mass to zero. These so-called semimetals are described by a massless Dirac equation and form a natural borderline between metals and insulators. A famous semimetal is graphene, while more recent three-dimensional examples are Weyl and Dirac semimetals [1,2]. Both were found to possess unusual transport properties including negative longitudinal magnetoresistance [3], and they carry topologically protected surface Fermi arcs [1].
Just like insulators, Weyl and Dirac semimetals fit nicely within high-energy physics theories, as the reference to Hermann Weyl and Paul Dirac signifies. One could even say that semimetallic materials allow us to emulate experiments which would be hardly achievable in particle physics. A natural question therefore is whether one may find materials where the electron dispersion does not have a counterpart in high-energy physics.
The key to resolve this question are symmetries. The high symmetry of vacuum constrains the form of the free electron Hamiltonian. While simplifying the problem, this also limits the variety of possible theories. On the contrary, condensed matter systems may possess much less symmetries, thus naturally permitting unusual terms in the Hamiltonian. This should naturally lead us beyond the established relativistic theories.
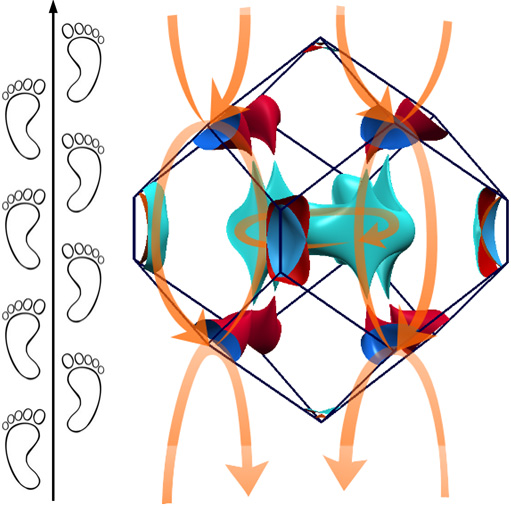
Indeed, such novel possibilities were recently uncovered. For example, study [4] identified systems where electrons behave as massless particles with an unusual value of spin. Another possibility has been identified in work [5] where the conduction and valence bands touch along lines rather than points, such that the concept of effective mass loses meaning altogether.
The quasiparticle excitations in such semimetals were named nodal-loop and nodal-chain fermions, and were predicted to exist in iridium fluoride, IrF4.
While many questions remain open, basic transport properties of such nodal-line semimetals were discussed in Ref. [5]. For example, the Fermi surface contains touching electron and hole pockets, and the material surfaces should exhibit anomalous surface Hall effect with topological transitions at special values of magnetic field. Furthermore, the bulk is predicted to exhibit a direction-selective chiral anomaly, thus nicely combining the properties of semimetals and ordinary metals.
Both Refs. [4,5] considered systems with non-symmorphic symmetries, i.e. point symmetries followed by a fractional shift. A simple one-dimensional example is offered by the footprints in the left part of the illustration. There, mirror has to be composed with a translation by one step to produce a so-called glide reflection. Such symmetries cause multiple bands to be “knotted” together, thus enforcing nodal points/lines and forbidding band insulators at certain integer fillings. Additionally, it has been predicted [6] that a non-symmorphic Mott insulator at such fillings has to acquire a topological order associated with a ground-state degeneracy.
The next step is up to experimentalist. The strong correlations of iridium electrons make it hard to predict whether the band structure picture remains valid in IrF4. If yes, we might expect an experimental confirmation of nodal-chain fermions in photoemission experiments. If it doesn’t, discovery of a topologically ordered Mott phase might be on the menu. The prospects are appealing either way.
Full title references
[1] “Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates,” X. Wan, A. M. Turner, A. Vishwanath, S. Y. Savrasov, Phys. Rev. B 83, 205101 (2011)
[2] “Discovery of a Three-Dimensional Topological Dirac Semimetal Na3Bi,” Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S.-K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain, Y. L. Chen, Science 343, 864 (2014)
[3] “Chiral anomaly and classical negative magnetoresistance of Weyl metals,” D. T. Son and B. Z. Spivak, Phys. Rev. B 88, 104412 (2013)
[4] “Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals,” B. Bradlyn, J. Cano, Z. Wang, M. G. Vergniory, C. Felser, R. J. Cava, B. A. Bernevig, Science 353, aaf5037 (2016)
[5] “Nodal-chain metals,” T. Bzdušek, Q.-S. Wu, A. Rüegg, M. Sigrist, A. A. Soluyanov, Nature 538, 75-58 (2016)
[6] “Topological order and absence of band insulators at integer fillings in non-symmorphic crystals,” S. A. Parameswaran, A. M. Turner, D. P. Arovas, A. Vishwanath, Nat. Phys. 9, 299-303 (2013)
Short references
[1] X. Wan, A. M. Turner, A. Vishwanath, S. Y. Savrasov, Phys. Rev. B 83, 205101 (2011)
[2] Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S.-K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain, Y. L. Chen, Science 343, 864 (2014)
[3] D. T. Son and B. Z. Spivak, Phys. Rev. B 88, 104412 (2013)
[4] B. Bradlyn, J. Cano, Z. Wang, M. G. Vergniory, C. Felser, R. J. Cava, B. A. Bernevig, Science 353, aaf5037 (2016)
[5] T. Bzdušek, Q.-S. Wu, A. Rüegg, M. Sigrist, A. A. Soluyanov, Nature 538, 75-58 (2016)
[6] S. A. Parameswaran, A. M. Turner, D. P. Arovas, A. Vishwanath, Nat. Phys. 9, 299-303 (2013)
Contact: Tomáš Bzdušek, (Tel. +41 44 633 25 80)
Read the ETHZ press release